3 Equilibrium constant Ka

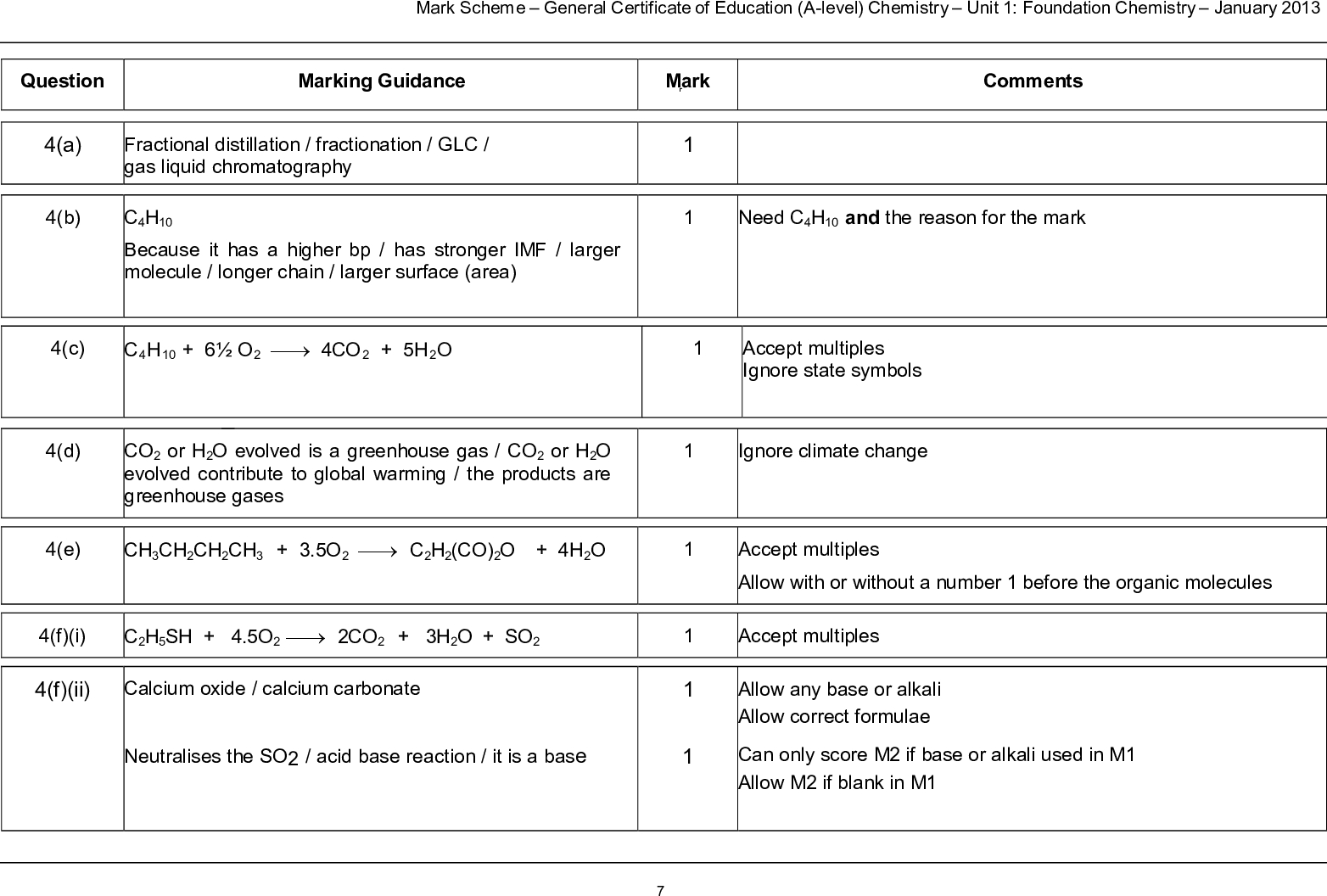
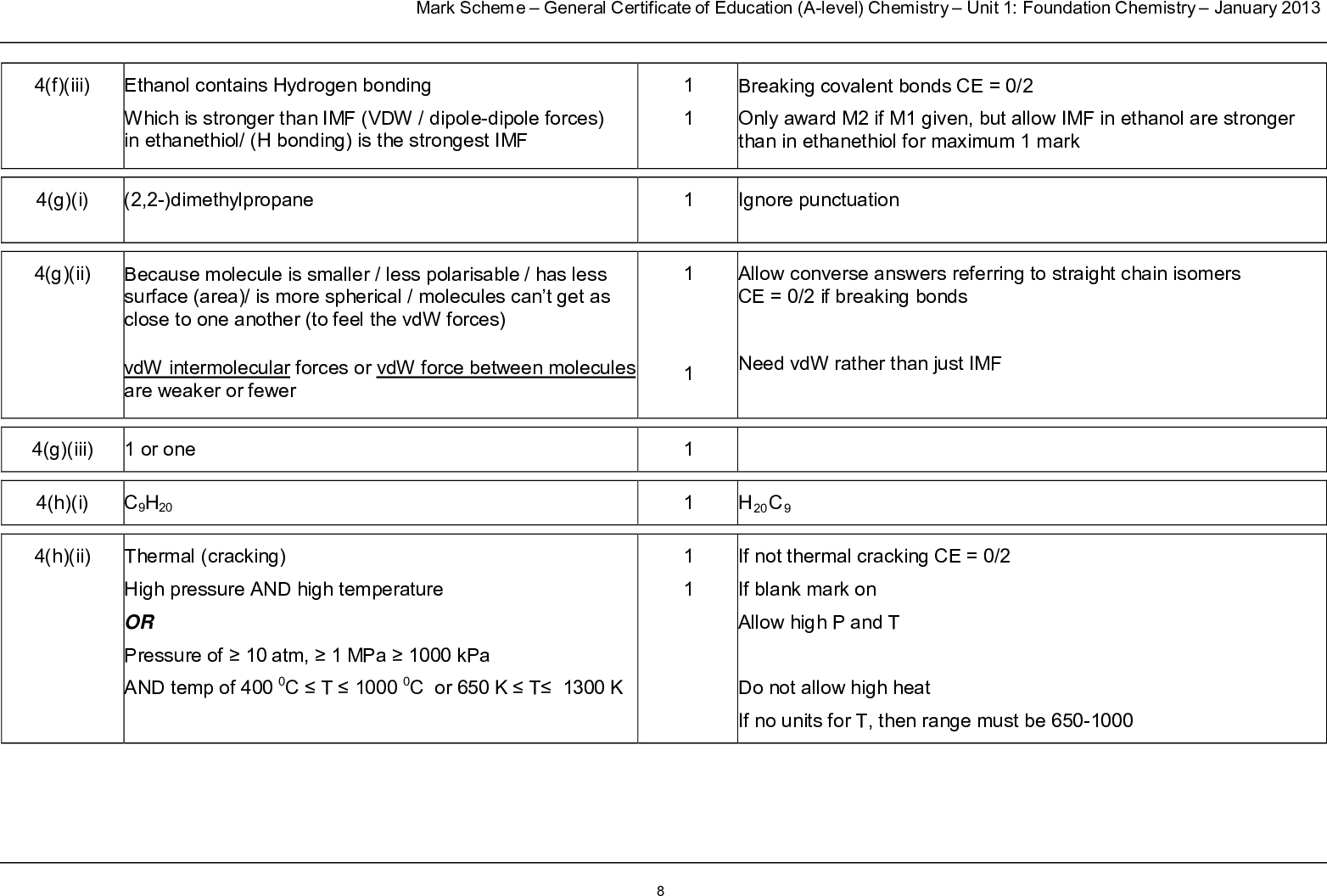
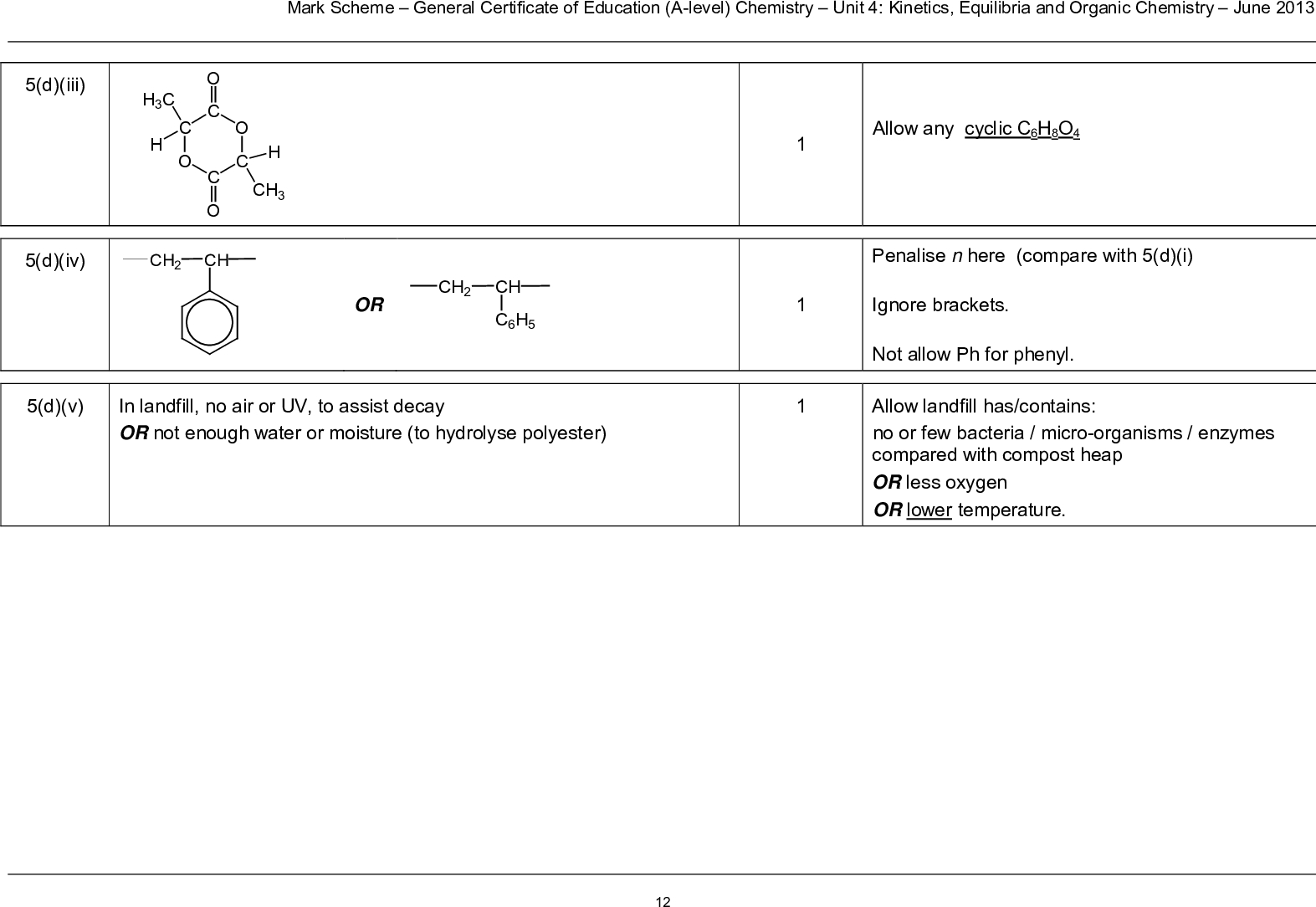
Weak acids Weak acids only slightly dissociate when dissolved in water, giving an equilibrium mixture HA + H2O (l) H3O+ (aq) + A- (aq) HA (aq) H+ (aq) + A- (aq) We can simplify this to [H+ (aq)][A- (aq)] [HA (aq)] Ka= Weak acids dissociation expression The Ka for ethanoic acid is 1.7 x 10-5 mol dm-3 . The larger ka the stronger the acid [H+ (aq)][CH3CH2CO2 – (aq)] [CH3CH2CO2H(aq)] Ka= CH3CH2CO2H(aq) H+ (aq) + CH3CH2CO2 – (aq) Example 4 Write equation for dissociation of propanoic acid and its ka expression Calculating pH of a weak acid To make the calculation easier two assumptions are made to simplify the Ka expression: 1) [H+ (aq)]eqm = [A- (aq)] eqm because they have dissociated according to a 1:1 ratio 2) As the amount of dissociation is small we assume that the initial concentration of the undissociated acid has remained constant. So [HA (aq) ] eqm = [HA(aq) ] initial [H+ (aq)][A- (aq)] [HA (aq)] Ka= Simplifies to [H+ (aq)]2 [HA (aq)] initial Ka= Example 5 What is the pH of a solution of 0.01M ethanoic acid (ka is 1.7 x 10-5 mol dm-3 )? CH3CO2H(aq) H+ (aq) + CH3CO2 – (aq) [H+ (aq)][CH3CO2 – (aq)] [CH3CO2H(aq)] Ka= [H+ (aq)]2 [CH3CO2H(aq)] initial Ka= [H+ (aq)]2 0.01 1.7x 10-5 = [H+ (aq)]2 = 1.7 x 10-5 x 0.01 [H+ (aq)] = √ 1.7 x 10-7 = 4.12 x 10-4 pH = – log [H+ ] = -log (4.12 x10-4 ) pH =3.38 Example 6 What is the concentration of propanoic acid with a pH of 3.52 (ka is 1.35 x 10-5 mol dm-3 )? CH3CH2CO2H(aq) H+ (aq) + CH3CH2CO2 – (aq) [H+ (aq)][CH3CH2CO2 – (aq)] [CH3CH2CO2H(aq)] Ka= [H+ (aq)]2 [CH3CH2CO2H(aq)] initial Ka= [0.000302]2 [CH3CH2CO2H(aq)] initial 1.35 x 10-5 = [CH3CH2CO2H(aq)] = 9.12 x 10-8 /1.35 x 10-5 [H+ ] = 1 x 10-3.52 = 0.000302M [CH3CH2CO2H(aq)] = 6.75 x 10-3 M pKa Sometimes Ka values are quoted as pKa values pKa = -log Ka so Ka = 10-pKa