The mole and Avogadro’s constant







3.1.2.1 Relative atomic mass and relative molecular mass
Relative atomic mass and relative molecular mass in terms of 12C. The term relative formula mass will be used for ionic compounds. Students should be able to: • define relative atomic mass (Ar ) • define relative molecular mass (Mr ).
3.1.2.2 The mole and the Avogadro constant
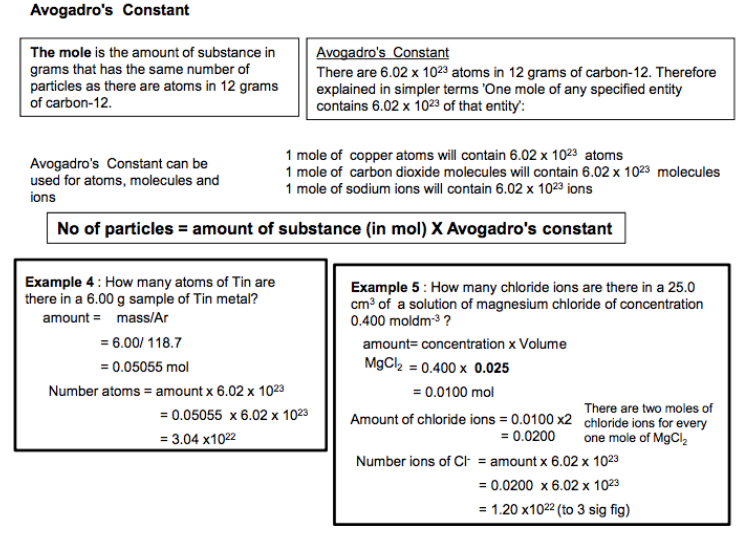
The Avogadro constant as the number of particles in a mole. The mole as applied to electrons, atoms, molecules, ions, formulas and equations. The concentration of a substance in solution, measured in mol dm–3. Students should be able to carry out calculations: • using the Avogadro constant • using mass of substance, Mr , and amount in moles • using concentration, volume and amount of substance in a solution. Students will not be expected to recall the value of the Avogadro constant.
3.1.2.3 The ideal gas equation
The ideal gas equation pV = nRT with the variables in SI units. Students should be able to use the equation in calculations. Students will not be expected to recall the value of the gas constant, R.
3.1.2.5 Balanced equations and associated calculations
Students should be able to use balanced equations to calculate: • masses
Empirical and molecular formulae



3.1.2.4 Empirical and molecular formula
Empirical formula is the simplest whole number ratio of atoms of each element in a compound. Molecular formula is the actual number of atoms of each element in a compound. The relationship between empirical formula and molecular formula. Students should be able to: • calculate empirical formula from data giving composition by mass or percentage by mass • calculate molecular formula from the empirical formula and relative molecular mass.
Balancing full equations
There must be the same number of atoms belonging to each element on each side of the equation. For example,
C+O2 → CO2
On the left there is one atom of carbon (C) and two atoms in a molecule of oxygen (O2). This must balance with the right: CO2 is one atom of carbon combined with two atoms of oxygen. If the equation is not balanced, only big numbers in front of various chemicals (ie in the spaces) to balance the equation. For example,
__Fe2O3 +__C →__Fe + __CO2
Numbers in subscript (ie 2 and 3 in Fe2O3) cannot be changed because during so will change the identity of the chemical (ie Fe2O3 is different from FeO).


3.1.2.5 Balanced equations and associated calculations
Equations (full and ionic).
Students should be able to:
• write balanced equations for reactions studied
• balance equations for unfamiliar reactions when reactants and products are specified.
Balancing ionic equations



3.1.2.5 Balanced equations and associated calculations
Equations (full and ionic).
Students should be able to:
• write balanced equations for reactions studied
• balance equations for unfamiliar reactions when reactants and products are specified.
Equations and quantities



3.1.2.5 Balanced equations and associated calculations
Students should be able to:
• concentrations and volumes for reactions in solutions.
Percentage yield and atom economy

3.1.2.5 Balanced equations and associated calculations

Students should be able to:
• percentage yields
• percentage atom economies
3.1.2.5 Balanced equations and associated calculationsPercentage atom economy is: molecular mass of desired product sum of molecular masses of all reactants × 100 Economic, ethical and environmental advantages for society and for industry of developing chemical processes with a high atom economy.
Students should be able to:
• percentage yields
• percentage atom economies
Reacting volume of gases

3.1.2.5 Balanced equations and associated calculations
Students should be able to:
• volumes of gases
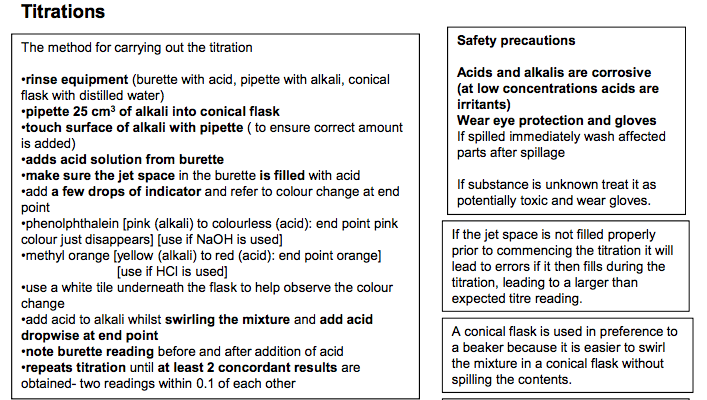
Required Practical 1: Volumetric solution and acid base titration




Making a solution
Weigh the sample bottle containing the required mass of solid on a 2 dp balance • Transfer to beaker and reweigh sample bottle • Record the difference in mass • Add 100cm3 of distilled water to the beaker. Use a glass rod to stir to help dissolve the solid. •Sometimes the substance may not dissolve well in cold water so the beaker and its contents could be heated gently until all the solid had dissolved. • Pour solution into a 250cm3 graduated flask via a funnel. • Rinse beaker and funnel and add washings from the beaker and glass rod to the volumetric flask. • make up to the mark with distilled water using a dropping pipette for last few drops. • Invert flask several times to ensure uniform solution. Alternatively the known mass of solid in the weighing bottle could be transferred to beaker, washed and washings added to the beaker. Remember to fill so the bottom of the meniscus sits on the line on the neck of the flask. With dark liquids like potassium manganate it can be difficult to see the meniscus. Titrations The method for carrying out the titration •rinse equipment (burette with acid, pipette with alkali, conical flask with distilled water) •pipette 25 cm3 of alkali into conical flask •touch surface of alkali with pipette ( to ensure correct amount is added) •adds acid solution from burette •make sure the jet space in the burette is filled with acid •add a few drops of indicator and refer to colour change at end point •phenolphthalein [pink (alkali) to colourless (acid): end point pink colour just disappears] [use if NaOH is used] •methyl orange [yellow (alkali) to red (acid): end point orange] [use if HCl is used] •use a white tile underneath the flask to help observe the colour change •add acid to alkali whilst swirling the mixture and add acid dropwise at end point •note burette reading before and after addition of acid •repeats titration until at least 2 concordant results are obtained- two readings within 0.1 of each other Recording results •Results should be clearly recorded in a table •Result should be recorded in full (i.e. both initial and final readings) •Record titre volumes to 2dp (0.05 cm3 ) Safety precautions Acids and alkalis are corrosive (at low concentrations acids are irritants) Wear eye protection and gloves If spilled immediately wash affected parts after spillage If substance is unknown treat it as potentially toxic and wear gloves. Working out average titre results Only make an average of the concordant titre results lf 2 or 3 values are within 0.10cm3 and therefore concordant or close then we can say results are accurate and reproducible and the titration technique is good/ consistent Testing batches In quality control it will be necessary to do titrations/testing on several samples as the amount/concentration of the chemical being tested may vary between samples. Titrating mixtures If titrating a mixture to work out the concentration of an active ingredient it is necessary to consider if the mixture contains other substances that have acid base properties. If they don’t have acid base properties we can titrate with confidence. Safely dealing with excess acid Sodium hydrogen carbonate (NaHCO3 ) and calcium carbonate (CaCO3 ) are good for neutralising excess acid in the stomach or acid spills because they are not corrosive and will not cause a hazard if used in excess. They also have no toxicity if used for indigestion remedies but the CO2 produced can cause wind. Magnesium hydroxide is also suitable for dealing with excess stomach acid as it has low solubility in water and is only weakly alkaline so not corrosive or dangerous to drink (unlike the strong alkali sodium hydroxide). It will also not produce any carbon dioxide gas. A conical flask is used in preference to a beaker because it is easier to swirl the mixture in a conical flask without spilling the contents. Common Titration Equations CH3CO2H + NaOH CH3CO2 -Na+ + H2O H2SO4 + 2NaOH Na2SO4 +2H2O HCl + NaOH NaCl +H2O NaHCO3 + HCl NaCl + CO2 + H2O Na2CO3 + 2HCl 2NaCl + CO2 + H2O Distilled water can be added to the conical flask during a titration to wash the sides of the flask so that all the acid on the side is washed into the reaction mixture to react with the alkali. It does not affect the titration reading as water does not react with the reagents or change the number of moles of acid added. If the jet space is not filled properly prior to commencing the titration it will lead to errors if it then fills during the titration, leading to a larger than expected titre reading. Indicators are generally weak acids so we only add a few drops of them. If too much is added it will affect the titration result. Calculating Apparatus Uncertainties Each type of apparatus has a sensitivity uncertainty •balance 0.001 g •volumetric flask 0.1 cm3 •25 cm3 pipette 0.1 cm3 •burette (start & end readings and end point ) 0.15 cm3 Calculate the percentage error for each piece of equipment used by % uncertainty = uncertainty x 100 Measurement made on apparatus e.g. for burette % uncertainty = 0.15/average titre result x100 To calculate the maximum percentage apparatus uncertainty in the final result add all the individual equipment uncertainties together. Reducing uncertainties in a titration Replacing measuring cylinders with pipettes or burettes which have lower apparatus uncertainty will lower the error To reduce the uncertainty in a burette reading it is necessary to make the titre a larger volume. This could be done by: increasing the volume and concentration of the substance in the conical flask or by decreasing the concentration of the substance in the burette. To decrease the apparatus uncertainties you can either decrease the sensitivity uncertainty by using apparatus with a greater resolution (finer scale divisions ) or you can increase the size of the measurement made. If looking at a series of measurements in an investigation the experiments with the smallest readings will have the highest experimental uncertainties. Reducing uncertainties in measuring mass Using a more accurate balance or a larger mass will reduce the uncertainty in weighing a solid Weighing sample before and after addition and then calculating difference will ensure a more accurate measurement of the mass added. Calculating the percentage difference between the actual value and the calculated value If we calculated an Mr of 203 and the real value is 214, then the calculation is as follows: Calculate difference 214-203 = 11 % = 11/214 x100 =5.41% If the %uncertainty due to the apparatus < percentage difference between the actual value and the calculated value then there is a discrepancy in the result due to other errors. If the %uncertainty due to the apparatus > percentage difference between the actual value and the calculated value then there is no discrepancy and all errors in the results can be explained by the sensitivity of the equipment. Uncertainty of a measurement using a burette. If the burette used in the titration had an uncertainty for each reading of +/– 0.05 cm3 then during a titration two readings would be taken so the uncertainty on the titre volume would be +/– 0.10 cm3 . Then often another 0.05 is added on because of uncertainty identifying the end point colour change. Uncertainty Uncertainty of a measurement using a burette. If the burette used in the titration had an uncertainty for each reading of +/– 0.05 cm3 then during a titration two readings would be taken so the uncertainty on the titre volume would be +/– 0.10 cm3 . Then often another 0.05 is added on because of uncertainty identifying the end point colour change The uncertainty of a reading (one judgement) is at least ±0.5 of the smallest scale reading. The uncertainty of a measurement (two judgements) is at least ±1 of the smallest scale reading. Readings and Measurements Readings the values found from a single judgement when using a piece of equipment Measurements the values taken as the difference between the judgements of two values (e.g. using a burette in a titration).
3.1.2.5 Balanced equations and associated calculations
Required practical 1
Make up a volumetric solution and carry out a simple acid–base titration.
Credits: Neil Goalby

