Bronsted-Lowry Acids and Bases

Bronsted-Lowry Definition of Acid – Base behaviour A Bronsted-Lowry acid is defined as a substance that can donate a proton. A Bronsted-Lowry base is defined as a substance that can accept a proton. HCl (g) + H2O (l) H3O+ (aq) + Cl- (aq) Acid 1 base 2 Acid 2 Base 1 Each acid is linked to a conjugate base on the other side of the equation. HNO3 + HNO2 ⇌ NO3 – + H2NO2+ Acid 1 Base 2 Base 1 Acid 2 HCOOH + CH3 (CH2 )2COOH ⇌ HCOO– + CH3 (CH2 )2COOH2+ Acid 1 Base 2 Base 1 Acid 2 In these reactions the substance with bigger Ka will act as the acid The acidic role of H+ in the reactions of acids with metals, carbonates, bases and alkalis acid + metal salt + hydrogen 2CH3CH2CO2H + Mg (CH3CH2COO)2Mg + H2 acid + alkali (NaOH) salt + water 2HNO2 + Ca(OH)2 Ca(NO2 )2 + 2H2O acid + carbonate (Na2CO3 ) salt + water + CO2 2CH3CO2H + Na2CO3 2CH3CO2 -Na+ + H2O + CO2 2H+ + Mg Mg2+ + H2 Ionic Equations H+ + OH– H2O 2H+ + CO3 2– H2O + CO2
/
~
~
~
/
5.1.3 Acids, bases and buffers

Brønsted–Lowry acids and bases (a) (i) a Brønsted–Lowry acid as a species that donates a proton and a Brønsted–Lowry base as a species that accepts a proton (see also 2.1.4 Acids) (ii) use of the term conjugate acid–base pairs (iii) monobasic, dibasic and tribasic acids Learners should be able to identify acid–base pairs in equations for acid–base equilibria. HSW1,7 Development of different models over time to explain acid–base behaviour. (b) the role of H+ in the reactions of acids with metals and bases (including carbonates, metal oxides and alkalis), using ionic equations (see also 2.1.4 c, 2.1.5 e)
Calculating pH




Calculating pH pH = – log [H+ ] Where [H+ ] is the concentration of hydrogen ions in the solution Calculating pH of strong acids Strong acids completely dissociate The concentration of hydrogen ions in a monoprotic strong acid will be the same as the concentration of the acid. For HCl and HNO3 the [H+ (aq)] will be the same as the original concentration of the acid. For 0.1M HCl the pH will be –log[0.1] =1.00 Always give pH values to 2d.p. In the exam Finding [H+ ] from pH [H+ ] = 1 x 10-pH On most calculators this is done by pressing Inv (or 2nd function) log – number(pH) Example 1 What is the concentration of HCl with a pH of 1.35? [H+ ] = 1 x 10-1.35 = 0.045M. Ionic Product for water [H+ (aq)][OH- (aq)] [H2O(l)] Kc= This equilibrium has the following equilibrium expression Kc x [H2O (l)] = [H+ (aq) ][OH- (aq)] Rearrange to Because [H2O (l)] is much bigger than the concentrations of the ions, we assume its value is constant and make a new constant Kw Kw = [H+ (aq) ][OH- (aq) ] Learn this expression At 25oC the value of Kw for all aqueous solutions is 1×10-14 mol2dm-6 The Kw expression can be used to calculate [H+ (aq)] ions if we know the [OH- (aq)] ions and vice versa Finding pH of pure water Pure water/ neutral solutions are neutral because the [H+ (aq) ] = [OH- (aq)] Using Kw = [H+ (aq) ][OH- (aq) ] then when neutral Kw = [H+ (aq) ]2 and [H+ (aq) ] = √ Kw At 25oC [H+ (aq) ] = √ 1×10-14 = 1×10-7 so pH = 7 At different temperatures to 25oC the pH of pure water changes. Le Chatelier’s principle can predict the change. The dissociation of water is endothermic (because bonds are broken) so increasing the temperature would push the equilibrium to the right giving a bigger concentration of H+ ions and a lower pH Example 2 : Calculate the pH of water at 50ºC given that Kw = 5.476 x 10-14 mol2 dm-6 at 50ºC [H+ (aq) ] = √ Kw = √ 5.476 x 10-14 =2.34 x 10-7 mol dm-3 pH = – log 2.34 x 10-7 = 6.6 It is still neutral though as [H+ (aq) ] = [OH- (aq)] N Goalby chemrevise.org Calculating pH of Strong Base For bases we are normally given the concentration of the hydroxide ion. To work out the pH we need to work out [H+ (aq)] using the kw expression. Strong bases completely dissociate into their ions NaOH Na+ + OHExample 3: What is the pH of the strong base 0.1M NaOH Assume complete dissociation. Kw = [H+ (aq)][OH- (aq)] = 1×10-14 [H+ (aq)] = kw/ [OH- (aq)] = 1×10-14 / 0.1 = 1×10-13 M pH = – log[1×10-13 ] =13.00. In all aqueous solutions and pure water the following equilibrium occurs: H2O (l) H+ (aq) + OH- (aq)Diluting an acid or alkali pH of diluted strong acid [H+ ] = [H+ ]old x old volume new volume pH = – log [H+ ] pH of diluted base [OH– ] = [OH– ]old x old volume new volume [H+ ] = Kw [OH– ] pH = – log [H+ ] Example 7 Calculate the new pH when 50.0 cm3 of 0.150 mol dm-3 HCl is mixed with 500 cm3 of water. H+ ] = [H+ ]old x old volume new volume 0.05 0.55 [H+ (aq)] = 0.150 x [H+ (aq)] = 0.0136 pH = – log [H+ ] = -log 0.0136 = 1.87
/
~
~
~
/
5.1.3 Acids, bases and buffers

pH and [H+(aq)] (d) use of the expression for pH as: pH = –log[H+] [H+] = 10–pH M0.1, M0.4, M2.2, M2.3, M2.4, M2.5 HSW8 pH as convenient terminology for communicating [H+]. (e) use of the expression for the ionic product of water, Kw M0.1, M0.4, M2.2, M2.3, M2.4 (f) calculations of pH, or related quantities, for: (i) strong monobasic acids (ii) strong bases, using Kw M0.1, M0.4, M2.2, M2.3, M2.4, M2.5
Equilibrium constant Ka


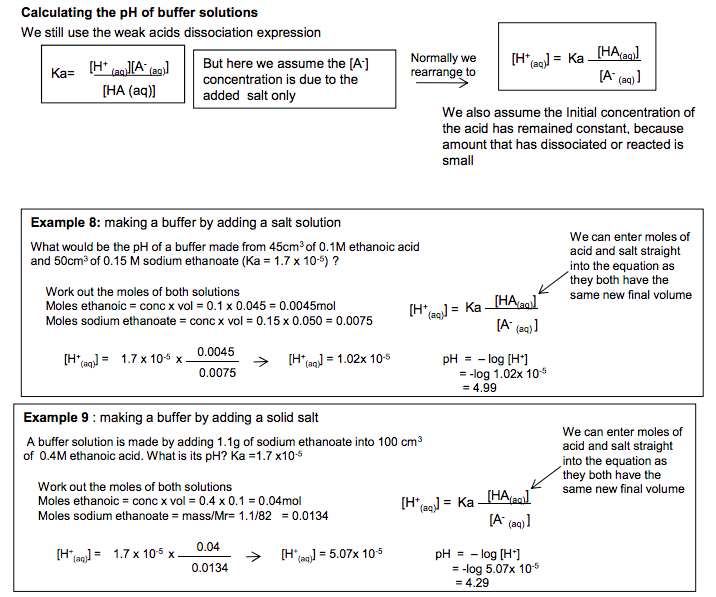
Weak acids Weak acids only slightly dissociate when dissolved in water, giving an equilibrium mixture HA + H2O (l) H3O+ (aq) + A- (aq) HA (aq) H+ (aq) + A- (aq) We can simplify this to [H+ (aq)][A- (aq)] [HA (aq)] Ka= Weak acids dissociation expression The Ka for ethanoic acid is 1.7 x 10-5 mol dm-3 . The larger ka the stronger the acid [H+ (aq)][CH3CH2CO2 – (aq)] [CH3CH2CO2H(aq)] Ka= CH3CH2CO2H(aq) H+ (aq) + CH3CH2CO2 – (aq) Example 4 Write equation for dissociation of propanoic acid and its ka expression Calculating pH of a weak acid To make the calculation easier two assumptions are made to simplify the Ka expression: 1) [H+ (aq)]eqm = [A- (aq)] eqm because they have dissociated according to a 1:1 ratio 2) As the amount of dissociation is small we assume that the initial concentration of the undissociated acid has remained constant. So [HA (aq) ] eqm = [HA(aq) ] initial [H+ (aq)][A- (aq)] [HA (aq)] Ka= Simplifies to [H+ (aq)]2 [HA (aq)] initial Ka= Example 5 What is the pH of a solution of 0.01M ethanoic acid (ka is 1.7 x 10-5 mol dm-3 )? CH3CO2H(aq) H+ (aq) + CH3CO2 – (aq) [H+ (aq)][CH3CO2 – (aq)] [CH3CO2H(aq)] Ka= [H+ (aq)]2 [CH3CO2H(aq)] initial Ka= [H+ (aq)]2 0.01 1.7x 10-5 = [H+ (aq)]2 = 1.7 x 10-5 x 0.01 [H+ (aq)] = √ 1.7 x 10-7 = 4.12 x 10-4 pH = – log [H+ ] = -log (4.12 x10-4 ) pH =3.38 Example 6 What is the concentration of propanoic acid with a pH of 3.52 (ka is 1.35 x 10-5 mol dm-3 )? CH3CH2CO2H(aq) H+ (aq) + CH3CH2CO2 – (aq) [H+ (aq)][CH3CH2CO2 – (aq)] [CH3CH2CO2H(aq)] Ka= [H+ (aq)]2 [CH3CH2CO2H(aq)] initial Ka= [0.000302]2 [CH3CH2CO2H(aq)] initial 1.35 x 10-5 = [CH3CH2CO2H(aq)] = 9.12 x 10-8 /1.35 x 10-5 [H+ ] = 1 x 10-3.52 = 0.000302M [CH3CH2CO2H(aq)] = 6.75 x 10-3 M pKa Sometimes Ka values are quoted as pKa values pKa = -log Ka so Ka = 10-pKa
/
~
~
~
/
5.1.3 Acids, bases and buffers



(c) (i) the acid dissociation constant, Ka, for the extent of acid dissociation (see also 2.1.4 b) (ii) the relationship between Ka and pKa M0.1, M0.2, M0.4, M2.3, M2.4, M2.5
(g) calculations of pH, Ka or related quantities, for a weak monobasic acid using approximations M0.1, M0.4, M2.1, M2.2, M2.3, M2.4, M2.5 Approximations for weak acid calculations: [HA]equilibrium ~ [HA]undissociated i.e. [HA] >> [H+] [H+] equilibrium ~ [A–] equilibrium i.e. negligible dissociation of H2O. Learners will not be required to solve quadratic equations.(h) limitations of using approximations to Ka related calculations for ‘stronger’ weak acids M0.3 Including reasons why [HA]equilibrium ~ [HA]undissociated may no longer be valid. HSW6 Understanding of the circumstances under which Ka approximations break down.
Buffer solutions
/
~
~
~
/
5.1.3 Acids, bases and buffers

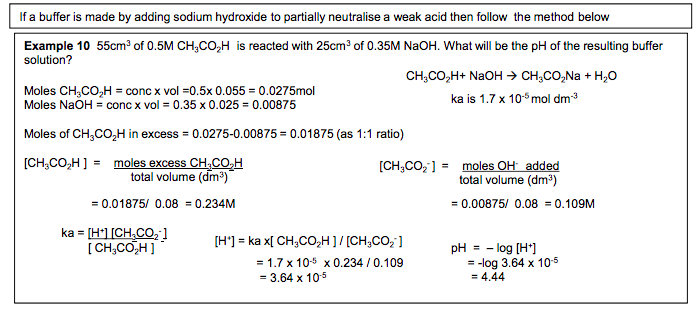
Buffers: action, uses and calculations (i) a buffer solution as a system that minimises pH changes on addition of small amounts of an acid or a base (j) formation of a buffer solution from: (i) a weak acid and a salt of the weak acid, e.g. CH3COOH/CH3COONa (ii) excess of a weak acid and a strong alkali, e.g. excess CH3COOH/NaOH (k) explanation of the role of the conjugate acid–base pair in an acid buffer solution, e.g. CH3COOH/CH3COO–, in the control of pH (l) calculation of the pH of a buffer solution, from the Ka value of a weak acid and the equilibrium concentrations of the conjugate acid–base pair; calculations of related quantities M0.1, M0.4, M2.2, M2.3, M2.4, M2.5 (m) explanation of the control of blood pH by the carbonic acid–hydrogencarbonate buffer system The H2CO3/HCO3 – buffer is present in blood plasma, maintaining a pH between 7.35 and 7.45
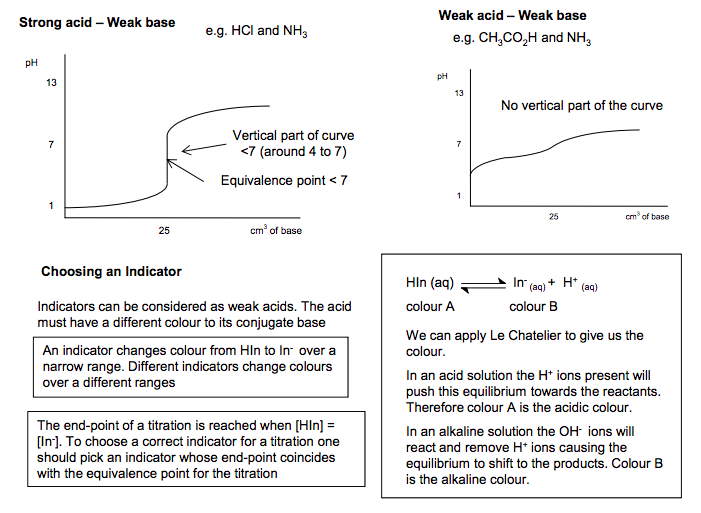
Titration curves PAG11
/
~
~
~
/
5.1.3 Acids, bases and buffers


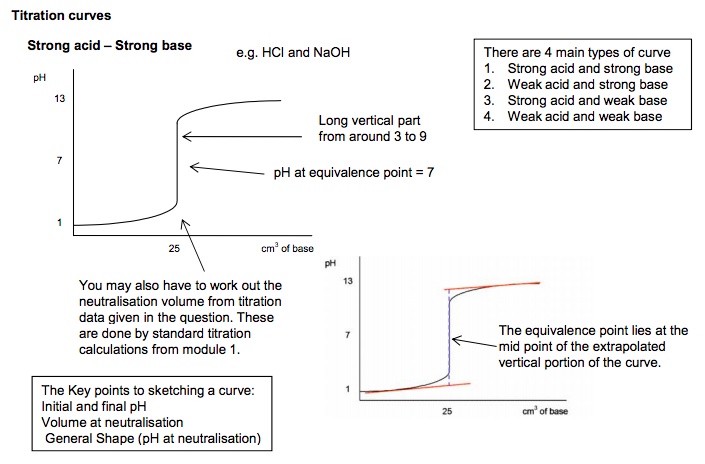
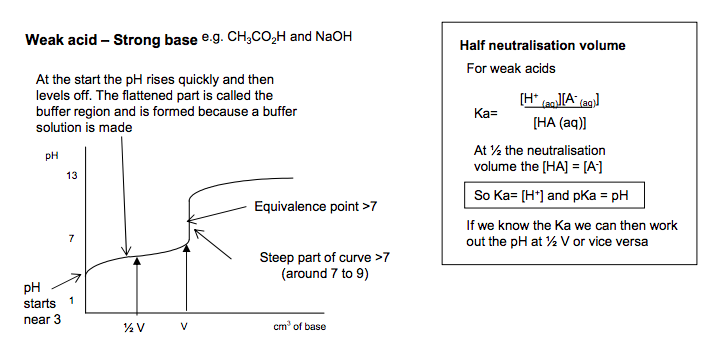
Neutralisation (n) pH titration curves for combinations of strong and weak acids with strong and weak bases, including: (i) sketch and interpretation of their shapes (ii) explanation of the choice of suitable indicators, given the pH range of the indicator (iii) explanation of indicator colour changes in terms of equilibrium shift between the HA and A– forms of the indicator M3.1 No indicator is suitable for a weak acid/weak base titration. The indicator should be considered as a weak acid, HA. (o) the techniques and procedures used when measuring pH with a pH meter. PAG11 HSW4 Opportunities to carry out experimental and investigative work.11 pH measurement • Measurement of pH Identifying unknown solutions via pH
measurements
5.1.3(o)
Credits: Neil Goalby