Amount of substance

The mole is the key concept for chemical calculations DEFINITION: The mole is the amount of substance in grams that has the same number of particles as there are atoms in 12 grams of carbon-12. DEFINITION: Relative atomic mass is the average mass of one atom compared to one twelfth of the mass of one atom of carbon-12 DEFINITION: Molar Mass is the mass in grams of 1 mole of a substance and is given the unit of g mol-1 molar gas volume (gas volume per mole, units dm3 mol–1 ) . This is the volume of 1 mole of a gas at a given temperature and pressure. All gases have this same volume. At room pressure (1atm) and room temperature 25oC the molar gas volume is 24 dm3 mol–1 amount = mass Mr For pure solids and gases Unit of Mass: grams Unit of amount : mol Example 1: What is the amount, in mol, in 35.0g of CuSO4? amount = mass/Mr = 35/ (63.5 + 32 +16 x4) = 0.219 mol Avogadro’s Constant There are 6.02 x 1023 atoms in 12 grams of carbon-12. Therefore explained in simpler terms ‘One mole of any specified entity contains 6.02 x 1023 of that entity’: 1 mole of copper atoms will contain 6.02 x 1023 atoms 1 mole of carbon dioxide molecules will contain 6.02 x 1023 molecules 1 mole of sodium ions will contain 6.02 x 1023 ions Avogadro’s Constant can be used for atoms, molecules and ions Molar Mass for a compound can be calculated by adding up the mass numbers(from the periodic table) of each element in the compound eg CaCO3 = 40.1 + 12.0 +16.0 x3 = 100.1 Significant Figures Give your answers to the same number of significant figures as the number of significant figures for the data you given in a question. If you are given a mixture of different significant figures, use the smallest. Calculation of reacting masses, gas volumes and mole concentrations Commonly in questions converting between quantities of substances reacting we will use more than just mass data. We might have the volume and concentration of a solution, or the volume of a gas. We need to adapt our existing method or reacting masses to include other quantities. Any of the equations below can be used to convert quantities into moles. amount = mass MolarMass 1. For pure solids, liquids and gases 3. For solutions Concentration = amount volume Unit of Mass: grams Unit of amount : mol Unit of concentration: mol dm-3 or M Unit of Volume: dm3 2. For Gases Gas Volume (dm3 )= amount x 24 This equation give the volume of a gas at room pressure (1atm) and room temperature 25oC. PV = nRT Or use the ideal gas equation to work out gas volumes at other temperatures and pressures PV = nRT Unit of Pressure (P):Pa Unit of Volume (V): m3 Unit of Temp (T): K n= moles R = 8.31 JK–1mol–1 Converting temperature oC  K add 273 Example 8: What is the mass of Cl2 gas that has a pressure of 100kPa, temperature 293K, volume 500cm3 . (R = 8.31 JK–1mol–1 ) moles = PV/RT = 100 000 x 0.0005 / (8.31 x 293) = 0.0205 mol 100 kPa = 100 000 Pa 500 cm3 = 0.0005 m3 Mass = moles x Mr = 0.0205 x (35.5 x2) = 1.46 g The ideal gas equation is a slightly more difficult way of working out a gas volume. It can calculate the volume for any temperature and pressure though so is a more useful method. The biggest problems students have with this equation is choosing and converting to the correct units, so pay close attention to the units. Ideal Gas Equation 5 Avogadro’s Constant There are 6.02 x 1023 atoms in 12 grams of carbon-12. Therefore explained in simpler terms ‘One mole of any specified entity contains 6.02 x 1023 of that entity’: N Goalby chemrevise.org The mole is the amount of substance in grams that has the same number of particles as there are atoms in 12 grams of carbon-12. Avogadro’s Constant 1 mole of copper atoms will contain 6.02 x 1023 atoms 1 mole of carbon dioxide molecules will contain 6.02 x 1023 molecules 1 mole of sodium ions will contain 6.02 x 1023 ions Avogadro’s Constant can be used for atoms, molecules and ions No of particles = amount of substance (in mol) X Avogadro’s constant Example 9 : How many atoms of Tin are there in a 6.00 g sample of Tin metal? amount = mass/Ar = 6/ 118.7 = 0.05055 mol Number atoms = amount x 6.02 x 1023 = 0.05055 x 6.02 x 1023 = 3.04 x1022 Example 10 : How many chloride ions are there in a 25.0 cm3 of a solution of magnesium chloride of concentration 0.400 moldm-3 ? Number ions of Cl- = amount x 6.02 x 1023 = 0.0200 x 6.02 x 1023 = 1.204 x1022 amount= concentration x Volume = 0.400 x 0.025 = 0.0100 mol MgCl2 Amount of chloride ions = 0.0100 x2 = 0.0200 There are two moles of chloride ions for every one mole of MgCl2. cm3  dm3 ÷ 1000 cm3  m3 ÷ 1000 000 dm3  m3 ÷ 1000 Simple mole calculations Some Simple calculations using above equations Example 6: What is the concentration of solution made by dissolving 5.00g of Na2CO3 in 250 cm3 water? amount = mass/Mr = 5 / (23 x2 + 12 +16 x3) = 0.0472 mol conc= amount/Volume = 0.0472 / 0.25 = 0.189 mol dm-3 I. Learn these equations carefully and what units to use in them. It is usually best to give your answers to 3sf. Example 7 : What is the volume in dm3 at room temperature and pressure of 50.0g of Carbon dioxide gas ? amount = mass/Mr = 50/ (12 + 16 x2) = 1.136 mol Gas Volume (dm3 )= amount x 24 = 1.136 x 24 = or 27.3 dm3 to 3 sig fig

Empirical formulae Step 1 : Divide each mass (or % mass) by the atomic mass of the element Step 2 : For each of the answers from step 1 divide by the smallest one of those numbers. Step 3: sometimes the numbers calculated in step 2 will need to be multiplied up to give whole numbers. These whole numbers will be the empirical formula. General method The same method can be used for the following types of data: 1. masses of each element in the compound 2. percentage mass of each element in the compound Example 2 : Calculate the empirical formula for a compound that contains 1.82g of K, 5.93g of I and 2.24g of O Step1: Calculate amount, in mol, by dividing each mass by the atomic mass of the element K = 1.82 / 39.1 I = 5.93/126.9 O = 2.24/16 = 0.0465 mol = 0.0467mol = 0.14 mol Step 2 For each of the answers from step 1 divide by the smallest one of those numbers. K = 0.0465/0.0465 I = 0.0467/0.0465 O = 0.14 / 0.0465 =1 = 1 = 3 Empirical formula =KIO3. Definition: An empirical formula is the simplest ratio of atoms of each element in the compound. Molecular formula from empirical formula Definition: A molecular formula is the actual number of atoms of each element in the compound. From the relative molecular mass (Mr) work out how many times the mass of the empirical formula fits into the Mr. Example 3. work out the molecular formula for the compound with an empirical formula of C3H6O and a Mr of 116 C3H6O has a mass of 58 The empirical formula fits twice into Mr of 116 So molecular formula is C6H12O2 The Mr does not need to be exact to turn an empirical formula into the molecular formula because the molecular formula will be a whole number multiple of the empirical formula

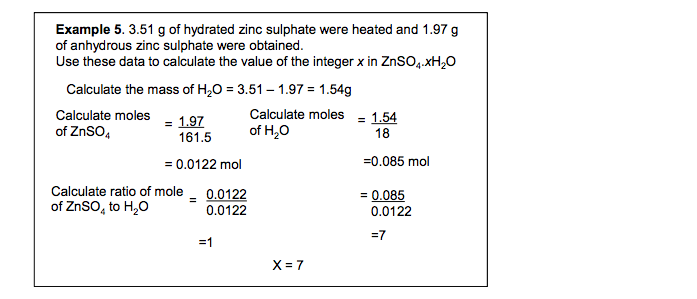
Example 5. 3.51 g of hydrated zinc sulphate were heated and 1.97 g of anhydrous zinc sulphate were obtained. Use these data to calculate the value of the integer x in ZnSO4 .xH2O Calculate the mass of H2O = 3.51 – 1.97 = 1.54g Calculate moles of ZnSO4 Calculate moles of H2O 1.97 161.5 = 1.54 18 = = 0.0122 mol =0.085 mol Calculate ratio of mole of ZnSO4 to H2O 0.0122 0.0122 = 0.085 0.0122 =1 =7 = X = 7

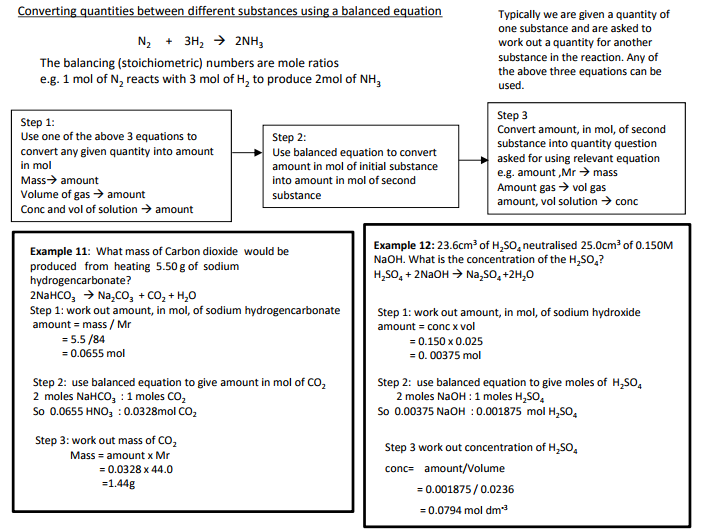
Converting quantities between different substances using a balanced equation The balancing (stoichiometric) numbers are mole ratios e.g. 1 mol of N2 reacts with 3 mol of H2 to produce 2mol of NH3 Typically we are given a quantity of one substance and are asked to work out a quantity for another substance in the reaction. Any of the above three equations can be used. Step 1: Use one of the above 3 equations to convert any given quantity into amount in mol Mass amount Volume of gas  amount Conc and vol of solution  amount Step 2: Use balanced equation to convert amount in mol of initial substance into amount in mol of second substance Step 3 Convert amount, in mol, of second substance into quantity question asked for using relevant equation e.g. amount ,Mr  mass Amount gas  vol gas amount, vol solution  conc Example 14: What mass of Copper would react completely with 150 cm3 of 1.60M nitric acid? 3Cu + 8HNO3  3Cu(NO3 )2 + 2NO + 4H2O Step 1: work out amount, in mol, of nitric acid amount = conc x vol = 1.60 x 0.15 = 0.24 mol Step 2: use balanced equation to give moles of Cu 8 moles HNO3 : 3 moles Cu So 0.24 HNO3 : 0.09 (0.24 x 3/8 ) mol Cu Step 3: work out mass of Cu Mass = amount x Mr = 0.09 x 63.5 =5.71g Example 12: 23.6cm3 of H2SO4 neutralised 25.0cm3 of 0.150M NaOH. What is the concentration of the H2SO4? H2SO4 + 2NaOH  Na2SO4 +2H2O Step 1: work out amount, in mol, of sodium hydroxide amount = conc x vol = 0.150 x 0.025 = 0. 00375 mol Step 2: use balanced equation to give moles of H2SO4 2 moles NaOH : 1 moles H2SO4 So 0.00375 NaOH : 0.001875 mol H2SO4 Step 3 work out concentration of H2SO4 conc= amount/Volume = 0.001875 / 0.0236 = 0.0794 mol dm-3 Example 11: What mass of Carbon dioxide would be produced from heating 5.50 g of sodium hydrogencarbonate? 2NaHCO3  Na2CO3 + CO2 + H2O Step 1: work out amount, in mol, of sodium hydrogencarbonate amount = mass / Mr = 5.5 /84 = 0.0655 mol Step 2: use balanced equation to give amount in mol of CO2 2 moles NaHCO3 : 1 moles CO2 So 0.0655 HNO3 : 0.0328mol CO2 Step 3: work out mass of CO2 Mass = amount x Mr = 0.0328 x 44.0 =1.44g N Goalby chemrevise.org 6 Example 13: What volume in cm3 of oxygen gas would be produced from the decomposition of 0.532 g of potassium chlorate(V)? 2KClO3  2 KCl + 3O2 Step 1: work out amount, in mol, of potassium chlorate(V)? amount = mass / Mr = 0.532 /122.6 = 0.00434 mol Step 3: work out volume of O2 Gas Volume (dm3 )= amount x 24 = 0.00651 x 24 = 0.156 dm3 = 156 cm3 Step 2: use balanced equation to give amount in mol of O2 2 moles KClO3 : 3 moles O2 So 0.00434 HNO3 : 0.00651mol O2

% Yield Example 7: 25.0g of Fe2O3 was reacted and it produced 10.0g of Fe. What is the percentage yield? Fe2O3 + 3CO  2Fe + 3 CO2 % yield = (actual yield/theoretical yield) x 100 = (10/ 17.48) x 100 =57.2% First calculate maximum mass of Fe that could be produced Step 1: work out amount in mol of Iron oxide amount = mass / Mr =25 / 159.6 = 0.1566 mol Step 2: use balanced equation to give moles of Fe 1 moles Fe2O3 : 2 moles Fe So 0.1566 Fe2O3 : 0.313moles Fe Step 3: work out mass of Fe Mass = amount x Mr = 0.313 x 55.8 =17.48g % yield in a process can be lowered through incomplete reactions, side reactions, losses during transfers of substances, losses during purification stages. % Atom Economy percentage atom economy Mass of useful products Mass of all reactants = x 100 Example 8 : What is the % atom economy for the following reaction where Fe is the desired product assuming the reaction goes to completion? Fe2O3 + 3CO  2Fe + 3 CO2 % atom economy = (2 x 55.8) (2 x 55.8 + 3×16) + 3 x (12+16) x 100 =45.8% Do take into account balancing numbers when working out % atom economy. Reactions where there is only one product where all atoms are used making product are ideal and have 100% atom economy. e.g. CH2=CH2 + H2  CH3CH3 Sustainable chemistry requires chemists to design processes with high atom economy that minimise production of waste products. If a process does have a side, waste product the economics of the process can be improved by selling the bi-product for other uses. percentage yield = x 100 actual yield theoretical yield

Making a solution Weighing can be made more accurate by weighing bottle again after it has been emptied into the beaker- or alternatively the weighing bottle could be washed and washings added to the beaker. Remember to fill so the bottom of the meniscus sits on the line on the neck of the flask. With dark liquids like potassium manganate it can be difficult to see the meniscus. •Weigh required mass of solute in a weighing bottle. • Tip contents into a beaker and add100cm3 of distilled water. Use a glass rod to stir to help dissolve the solid. •Sometimes the substance may not dissolve well in cold water so the beaker and its contents could be heated gently until all the solid had dissolved. •Pour solution into a 250cm3 graduated flask via a funnel. Rinse beaker and funnel and add washings from the beaker and glass rod to the volumetric flask. •make up to the mark with distilled water using a dropping pipette for last few drops. • Invert flask several times to ensure uniform solution.

The water of crystallisation in calcium sulphate crystals can be removed as water vapour by heating as shown in the following equation. CaSO4 .xH2O(s) → CaSO4 (s) + xH2O(g) Method. •Weigh an empty clean dry crucible and lid . •Add 2g of hydrated calcium sulphate to the crucible and weigh again •Heat strongly with a Bunsen for a couple of minutes •Allow to cool •Weigh the crucible and contents again •Heat crucible again and reweigh until you reach a constant mass ( do this to ensure reaction is complete). Small amounts the solid , such as 0.100 g, should not be used in this experiment as errors in weighing are too high. Large amounts of hydrated calcium sulphate, such as 50g, should not be used in this experiment as the decomposition is like to be incomplete. The lid improves the accuracy of the experiment as it prevents loss of solid from the crucible but should be loose fitting to allow gas to escape. The crucible needs to be dry otherwise a wet crucible would give an inaccurate result. It would cause mass loss to be too large as water would be lost when heating. Heating in a crucible This method could be used for measuring mass loss in various thermal decomposition reactions and also for mass gain when reacting magnesium in oxygen.N Goalby chemrevise.org A Hydrated salt contains water of crystallisation H. Cu(NO3 )2 .6H2O hydrated copper (II) nitrate(V). Cu(NO3 )2 Anhydrous copper (II) nitrate(V). Example 4 Na2SO4 . xH2O has a molar mass of 322.1, Calculate the value of x Molar mass xH2O = 322.1 – (23×2 + 32.1 + 16×4) = 180 X = 180/18 =10