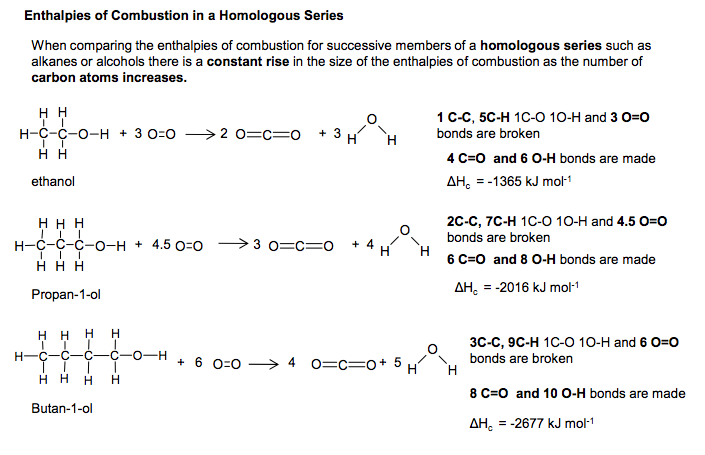
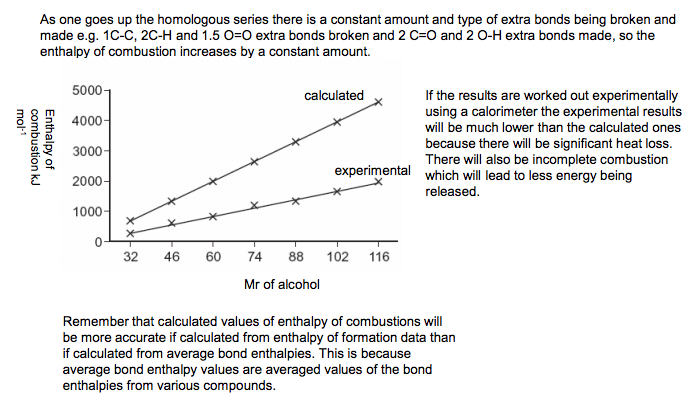
Definition: Enthalpy change is the amount of heat energy taken in or given out during any change in a system provided the pressure is constant.In an exothermic change energy is transferred from the system (chemicals) to the surroundings. The products have less energy than the reactants.If an enthalpy change occurs then energy is transferred between system and surroundings. The system is the chemicals and the surroundings is everything outside the chemicals. In an endothermic change, energy is transferred from the surroundings to the system (chemicals). They require an input of heat energy e.g. thermal decomposition of calcium carbonate The products have more energy than the reactantsIn an exothermic reaction the ∆H is negative. Common oxidation exothermic processes are the combustion of fuels and the oxidation of carbohydrates such as glucose in respiration. In an endothermic reaction the ∆H is positive. Standard Enthalpy Change of Formation When an enthalpy change is measured at standard conditions the symbol is used Eg ∆H The standard enthalpy change of formation of a compound is the enthalpy change when 1 mole of the compound is formed from its elements under standard conditions (298K and 100kpa), all reactants and products being in their standard states. Symbol ∆fH Mg (s) + Cl2 (g) � MgCl2 (s) 2Fe (s) + 1.5 O2 (g) � Fe2O3 (s) The enthalpy of formation of an element = 0 kJ mol-1 Standard Enthalpy Change of Combustion The standard enthalpy of combustion of a substance is defined as the enthalpy change that occurs when one mole of a substance is combusted completely in oxygen under standard conditions. (298K and 100kPa), all reactants and products being in their standard states. Symbol ∆cH CH4 (g) + 2O2 (g)� CO2 (g) + 2 H2O (l) Incomplete combustion will lead to soot (carbon), carbon monoxide and water. It will be less exothermic than complete combustion. Enthalpy changes are normally quoted at standard conditions. Standard conditions are: • 100 kPa pressure • 298 K (room temperature or 25oC) • Solutions at 1mol dm-3 • all substances should have their normal state at 298K

3.1.4.1 Enthalpy change
Reactions can be endothermic or exothermic. Enthalpy change (∆H) is the heat energy change measured under conditions of constant pressure. Standard enthalpy changes refer to standard conditions ie 100 kPa and a stated temperature (eg ∆H298 Ɵ). Students should be able to: • define standard enthalpy of combustion (∆c HƟ) • define standard enthalpy of formation (∆f HƟ).




. Calculating the enthalpy change of reaction, ∆Hr from experimental data General method 1. Using q= m x cp x ∆T calculate energy change for quantities used 2. Work out the moles of the reactants used. For a reaction in solution we use the following equation energy change = mass of solution x heat capacity x temperature change Q (J) = m (g) x cp (J g-1K-1) x ∆T ( K) This equation will only give the energy for the actual quantities used. Normally this value is converted into the energy change per mole of one of the reactants. (The enthalpy change of reaction, ∆Hr ) 3. Divide q by the number of moles of the reactant not in excess to give ∆H 4. Add a sign and unit (divide by a thousand to convert Jmol-1 to kJmol-1 The heat capacity of water is 4.18 J g-1K-1. In any reaction where the reactants are dissolved in water we assume that the heat capacity is the same as pure water. Also assume that the solutions have the density of water, which is 1g cm-3. Eg 25cm3 will weigh 25 g Example 1. Calculate the enthalpy change of reaction for the reaction where 25cm3 of 0.2 M copper sulphate was reacted with 0.01mol (excess of zinc). The temperature increased 7oC . Step 1: Calculate the energy change for the amount of reactants in the test tube. Q = m x cp x ∆T Q = 25 x 4.18 x 7 Q = 731.5 J Step 2 : calculate the number of moles of the reactant not in excess. moles of CuSO4 = conc x vol = 0.2 x 25/1000 = 0.005 mol If you are not told what is in excess, then you need to work out the moles of both reactants and work out using the balanced equation which one is in excess. Step 3 : calculate the enthalpy change per mole which is often called ∆H (the enthalpy change of reaction) ∆H = Q/ no of moles = 731.5/0.005 = 146300 J mol-1 = 146 kJ mol-1 to 3 sf Finally add in the sign to represent the energy change: if temp increases the reaction is exothermic and is given a minus sign e.g. –146 kJ mol-1 Remember in these questions: sign, unit, 3 sig figs. Example 2. 25cm3 of 2M HCl was neutralised by 25cm3 of 2M NaOH. The Temperature increased 13.5oC What was the energy change per mole of HCl? Step 1: Calculate the energy change for the amount of reactants in the test tube. Q = m x cp x ∆T Q = 50 x 4.18 x13.5 Q = 2821.5 J Step 2 : calculate the number of moles of the HCl. moles of HCl = conc x vol = 2 x 25/1000 = 0. 05 mol Step 3 : calculate ∆H the enthalpy change per mole which might be called the enthalpy change of neutralisation ∆H = Q/ no of moles = 2821.5/0.05 = 564300 J mol-1 = -56.4 kJ mol-1 to 3 sf Exothermic and so is given a minus sign Remember in these questions: sign, unit, 3 sig figs. Note the mass is the mass of the copper sulphate solution only. Do not include mass of zinc powder. Note the mass equals the mass of acid + the mass of alkali, as they are both solutions. Example 3. Calculate the enthalpy change of combustion for the reaction where 0.65g of propan-1-ol was completely combusted and used to heat up 150g of water from 20.1 to 45.5oC Step 1: Calculate the energy change used to heat up the water. Q = m x cp x ∆T Q = 150 x 4.18 x 25.4 Q = 15925.8 J Step 2 : calculate the number of moles of alcohol combusted. moles of propan-1-ol = mass/ Mr = 0.65 / 60 = 0.01083 mol Step 3 : calculate the enthalpy change per mole which is called ∆Hc (the enthalpy change of combustion) ∆H = Q/ no of moles = 15925.8/0.01083 = 1470073 J mol-1 = 1470 kJ mol-1 to 3 sf Finally add in the sign to represent the energy change: if temp increases the reaction is exothermic and is given a minus sign eg –1470 kJ mol-1 Remember in these questions: sign, unit, 3 sig figs. Note the mass is the mass of water in the calorimeter and not the alcohol Enthalpies of combustion can be calculated by using calorimetry. Generally the fuel is burnt and the flame is used to heat up water in a metal cup. Measuring Enthalpies of Combustion using Calorimetry

3.1.4.2 Calorimetry
The heat change, q, in a reaction is given by the equation q = mc∆T where m is the mass of the substance that has a temperature change ∆T and a specific heat capacity c. Students should be able to: • use this equation to calculate the molar enthalpy change for a reaction • use this equation in related calculations. Students will not be expected to recall the value of the specific heat capacity, c, of a substance.


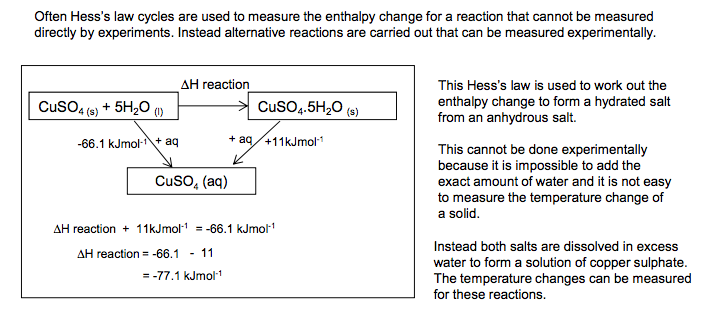
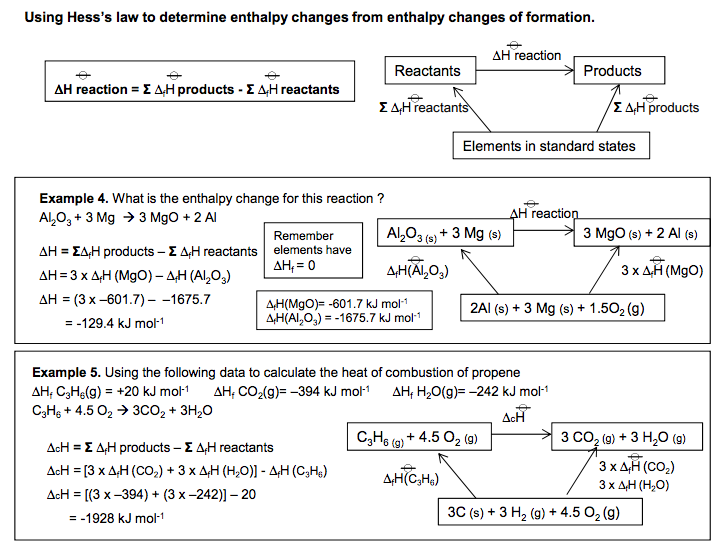
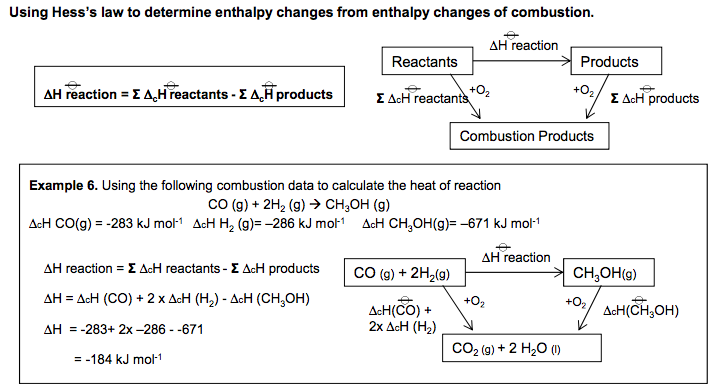
3.1.4.3 Applications of Hess’s law
Hess’s law. Students should be able to use Hess’s law to perform calculations, including calculation of enthalpy changes for reactions from enthalpies of combustion or from enthalpies of formation.
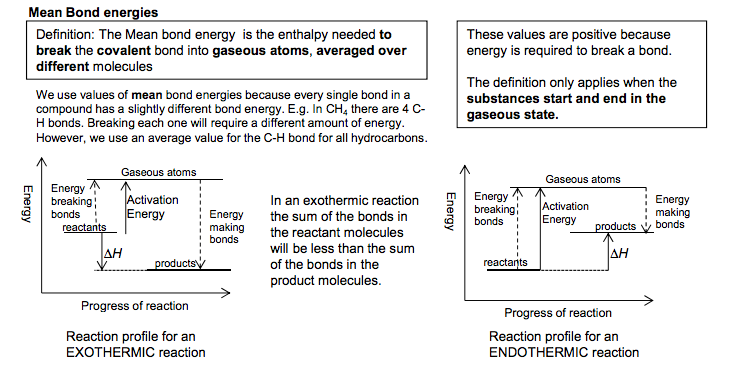
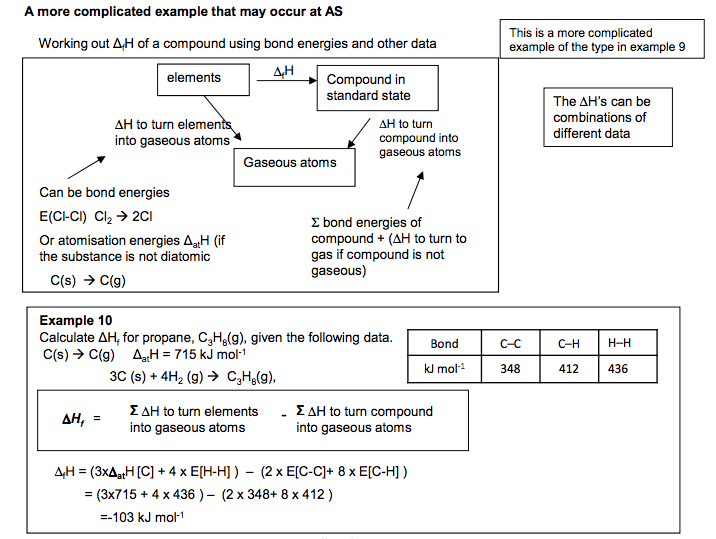
3.1.4.4 Bond enthalpies
Mean bond enthalpy. Students should be able to: • define the term mean bond enthalpy • use mean bond enthalpies to calculate an approximate value of ∆H for reactions in the gaseous phase • explain why values from mean bond enthalpy calculations differ from those determined using Hess’s law.



Errors in this method • Heat losses from calorimeter • Incomplete combustion of fuel • Incomplete transfer of heat • Evaporation of fuel after weighing • Heat capacity of calorimeter not included • Measurements not carried out under standard conditions as H2O is gas, not liquid, in this experiment. Calorimetric method
General method • washes the equipment (cup and pipettes etc) with the solutions to be used • dry the cup after washing • put polystyrene cup in a beaker for insulation and support • clamp thermometer into place making sure the thermometer bulb is immersed in liquid • measure the initial temperatures of the solution or both solutions if 2 are used • transfers reagents to cup. If a solid reagent is used then add the solution to the cup first and then add the solid weighed out on a balance. • stirs mixture • Measures final temperature One type of experiment is one in which substances are mixed in an insulated container and the temperature rise measured. This could be a solid dissolving or reacting in a solution or it could be two solutions reacting together • heat transfer from surroundings (usually loss) • approximation in specific heat capacity of solution. The method assumes all solutions have the heat capacity of water. • neglecting the specific heat capacity of the calorimeter- we ignore any heat absorbed by the apparatus. • reaction or dissolving may be incomplete or slow. • Density of solution is taken to be the same as water If the reaction is slow then the exact temperature rise can be difficult to obtain as cooling occurs simultaneously with the reaction To counteract this we take readings at regular time intervals and extrapolate the temperature curve/line back to the time the reactants were added together. We also take the temperature of the reactants for a few minutes before they are added together to get a better average temperature. If the two reactants are solutions then the temperature of both solutions need to be measured before addition and an average temperature is used.
3.1.4.2 Calorimetry
Required practical 2
Measurement of an enthalpy change.

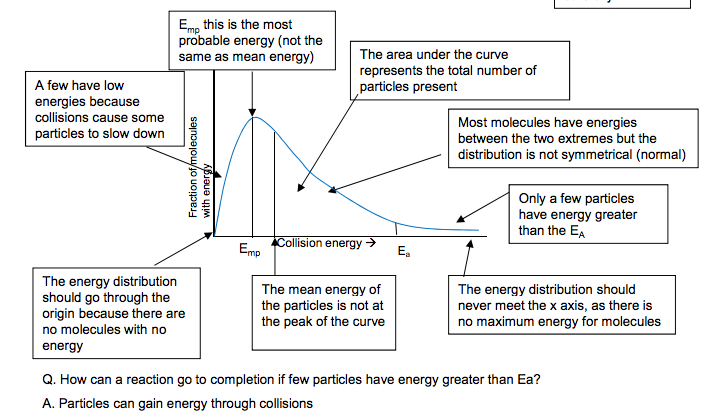
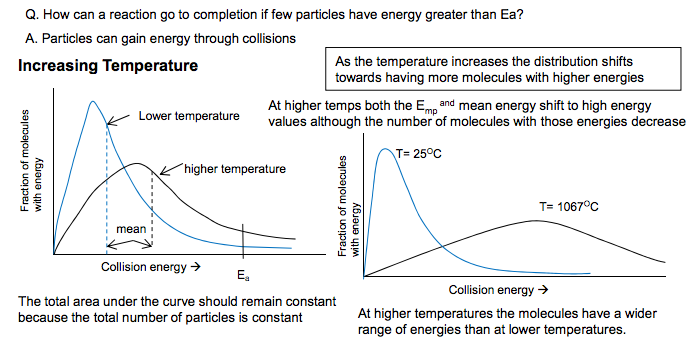
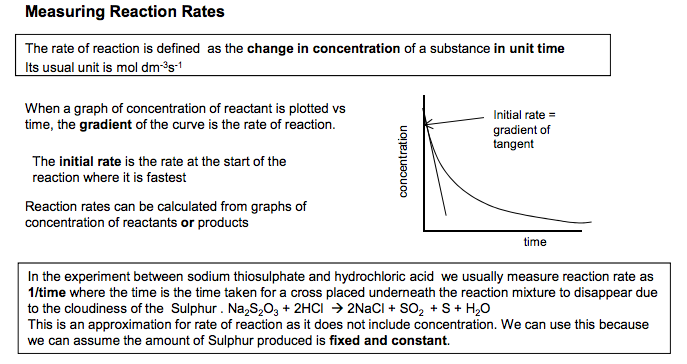

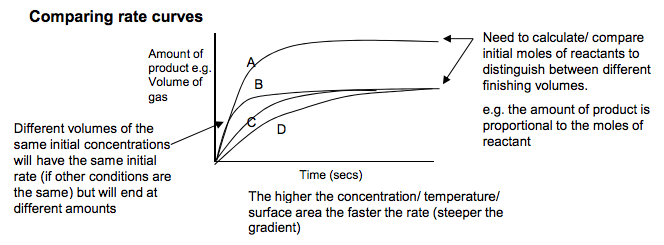
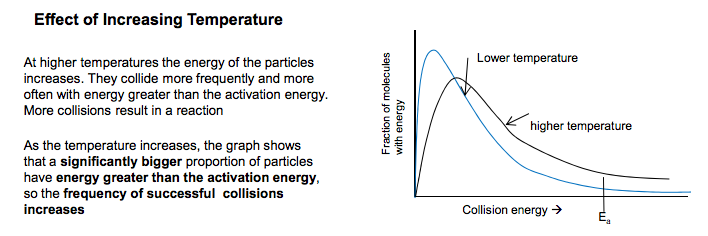
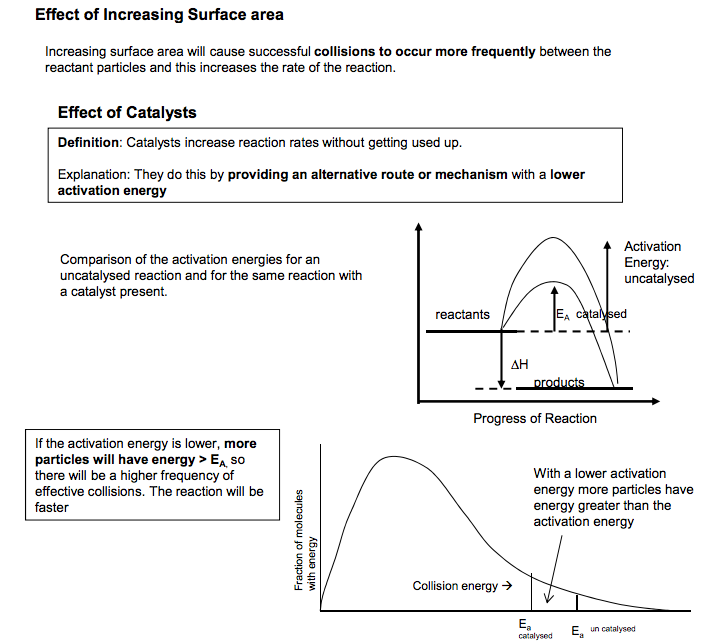
The Activation Energy is defined as the minimum energy which particles need to collide to start a reaction Maxwell Boltzmann Distribution The Maxwell-Boltzmann energy distribution shows the spread of energies that molecules of a gas or liquid have at a particular temperature Learn this curve carefully The energy distribution should go through the origin because there are no molecules with no energy The energy distribution should never meet the x axis, as there is no maximum energy for molecules The mean energy of the particles is not at the peak of the curve The area under the curve represents the total number of A few have low particles present energies because collisions cause some particles to slow down Only a few particles have energy greater than the EA Most molecules have energies between the two extremes but the distribution is not symmetrical (normal) Q. How can a reaction go to completion if few particles have energy greater than Ea? A. Particles can gain energy through collisions Emp this is the most probable energy (not the same as mean energy) Increasing Temperature As the temperature increases the distribution shifts towards having more molecules with higher energies The total area under the curve should remain constant because the total number of particles is constant At higher temperatures the molecules have a wider range of energies than at lower temperatures. At higher temps both the Emp and mean energy shift to high energy values although the number of molecules with those energies decrease 1.5 Kinetics Ea Collision energy � Fraction of molecules with energy higher temperature Lower temperature Ea Collision energy � Fraction of molecules with energy mean Collision energy � T= 25OC T= 1067OC Fraction of molecules with energy reactants products Activation Energy: EA ∆H Progress of Reaction Energy Reactions can only occur when collisions take place between particles having sufficient energy. The energy is usually needed to break the relevant bonds in one or either of the reactant molecules. This minimum energy is called the Activation Energy 1 Emp N Goalby chemrevise.org Measuring Reaction Rates The rate of reaction is defined as the change in concentration of a substance in unit time Its usual unit is mol dm-3s -1 When a graph of concentration of reactant is plotted vs time, the gradient of the curve is the rate of reaction. The initial rate is the rate at the start of the reaction where it is fastest Reaction rates can be calculated from graphs of concentration of reactants or products Effect of Increasing Concentration and Increasing Pressure At higher concentrations(and pressures) there are more particles per unit volume and so the particles collide with a greater frequency and there will be a higher frequency of effective collisions. If concentration increases, the shape of the energy distribution curves do not change (i.e. the peak is at the same energy) so the Emp and mean energy do not change They curves will be higher, and the area under the curves will be greater because there are more particles More molecules have energy > EA (although not a greater proportion) Comparing rate curves Need to calculate/ compare initial moles of reactants to distinguish between different finishing volumes. e.g. the amount of product is proportional to the moles of reactant Different volumes of the same initial concentrations will have the same initial rate (if other conditions are the same) but will end at different amounts The higher the concentration/ temperature/ surface area the faster the rate (steeper the gradient) In the experiment between sodium thiosulphate and hydrochloric acid we usually measure reaction rate as 1/time where the time is the time taken for a cross placed underneath the reaction mixture to disappear due to the cloudiness of the Sulphur . Na2S2O3 + 2HCl � 2NaCl + SO2 + S + H2O This is an approximation for rate of reaction as it does not include concentration. We can use this because we can assume the amount of Sulphur produced is fixed and constant. Higher concentration Ea Collision energy � Number of molecules with energy lower concentration Initial rate = gradient of tangent time concentration Amount of product e.g. Volume of gas Time (secs) A B C D Note: If a question mentions a doubling of concentration/rate then make sure you mention double the number of particles per unit volume and double the frequency of effective collisions. N Goalby chemrevise.org 2 Effect of Increasing Surface area Increasing surface area will cause successful collisions to occur more frequently between the reactant particles and this increases the rate of the reaction. Effect of Catalysts Definition: Catalysts increase reaction rates without getting used up. Explanation: They do this by providing an alternative route or mechanism with a lower activation energy Comparison of the activation energies for an uncatalysed reaction and for the same reaction with a catalyst present. If the activation energy is lower, more particles will have energy > EA, so there will be a higher frequency of effective collisions. The reaction will be faster Effect of Increasing Temperature At higher temperatures the energy of the particles increases. They collide more frequently and more often with energy greater than the activation energy. More collisions result in a reaction As the temperature increases, the graph shows that a significantly bigger proportion of particles have energy greater than the activation energy, so the frequency of successful collisions increases higher temperature Lower temperature Ea Collision energy � Fraction of molecules with energy Ea catalysed Fraction of molecules with energy Collision energy � Ea un catalysed With a lower activation energy more particles have energy greater than the activation energy reactants Activation Energy: uncatalysed ∆H Progress of Reaction EA catalysed 3 products





3.1.5.1 Collision theory
Reactions can only occur when collisions take place between particles having sufficient energy. This energy is called the activation energy. Students should be able to: • define the term activation energy • explain why most collisions do not lead to a reaction.
3.1.5.2 Maxwell–Boltzmann distribution
Maxwell–Boltzmann distribution of molecular energies in gases. Students should be able to draw and interpret distribution curves for different temperatures.
3.1.5.3 Effect of temperature on reaction rate
Meaning of the term rate of reaction. The qualitative effect of temperature changes on the rate of reaction. Students should be able to use the Maxwell–Boltzmann distribution to explain why a small temperature increase can lead to a large increase in rate.
3.1.5.4 Effect of concentration and pressure
The qualitative effect of changes in concentration on collision frequency. The qualitative effect of a change in the pressure of a gas on collision frequency. Students should be able to explain how a change in concentration or a change in pressure influences the rate of a reaction.
3.1.5.5 Catalysts
A catalyst is a substance that increases the rate of a chemical reaction without being changed in chemical composition or amount. Catalysts work by providing an alternative reaction route of lower activation energy. Students should be able to use a Maxwell–Boltzmann distribution to help explain how a catalyst increases the rate of a reaction involving a gas.




A-level Chemistry exemplar for required practical No. 3 Investigation of how the rate of a reaction changes with temperature: To investigate how the rate of the reaction of sodium thiosulfate with hydrochloric acid changes as the temperature of the reaction is changed. Introduction Sodium thiosulfate reacts with hydrochloric acid according to the equation Na2S2O3(aq) + 2HCl(aq) → 2NaCl(aq) + SO2(g) + S(s) The reaction produces a precipitate of sulfur. The rate of this reaction can be monitored by measuring the time taken for a fixed amount of sulfur to be produced. An easy method to do this is by timing how long it takes for a cross, marked on the bottom of the reaction vessel, to disappear as it is obscured by the sulfur precipitate. Dilute hydrochloric acid will be added to sodium thiosulfate solution at different temperatures in a series of experiments. This table shows the approximate temperatures for five experiments. Experiment 1 2 3 4 5 Approximate temperature / °C room* ~25 ~35 ~45 ~55** [* The temperature of the room is likely to be 15 to 18 °C] [** The temperature must not exceed 55 °C] It is not necessary for these exact temperatures to be used although the temperature used must not exceed 55 °C. However, the actual temperature at which each experiment is carried out must be known as accurately as possible. One way that this can be achieved is to measure both the initial temperature and the final temperature and then use a mean temperature when plotting your graph. Requirements In addition to general laboratory apparatus, each student needs: thermometer (–10 °C to 110 °C) 400 cm3 beaker (for use as a water bath) plastic container with lid 2 glass tubes to hold 12–14 cm3 of liquid 0.05 mol dm–3 (or 40 g dm –3 ) sodium thiosulfate solution 1.0 mol dm–3 hydrochloric acid (or 0.5 mol dm–3 sulfuric acid) 10 cm3 measuring cylinder plastic graduated pipette stopwatch graph paper. A lid is advised in this experiment. Two holes should be made in the lid using a hot wide cork borer. These holes should securely hold the glass tubes and vertically in the plastic container. A cross should be marked on the inside base of the plastic container below one of the larger holes using a permanent black marker pen. Alternatives include using clear A4 plastic wallets to use as a lid over the plastic container. Also, rather than marking the bottom of the plastic container directly, a laminated sheet marked with a black cross could be used Caution: the CLEAPSS Hazcard states ‘sulfur dioxide is produced in this reaction’ and ‘known sufferers of asthma should be closely monitored’. Centres are advised to ensure that the investigation is carried out in a well-ventilated room and that appropriate measures are taken to dispose of waste solutions. Stop baths – containers of sodium carbonate solution and phenolphthalein should be available to students so that the acid and sulfur dioxide can be neutralised (immediately, if required, during the practical and) after the experiment has finished. Once the colour of the solution in the stop bath changes, the sodium carbonate has been used up and the stop bath will need to be replenished. The stop bath should be placed in a fume cupboard, if available. Analysing the data In these experiments at different temperatures, the concentrations of all the reactants are the same. You are investigating the time taken to produce the same amount of sulfur at different temperatures. If you were to plot a graph of the amount of sulfur produced against time, it would initially be a straight line because the reaction has only just started. Therefore, the initial rate of reaction = (amount of sulfur)/time so the initial rate of reaction is proportional to 1/time ( 1 ). AS analysis calculate the mean temperature of each reaction mixture for each of the five temperatures, calculate 1 to 3 significant figures, where t is the time taken for the cross to be obscured plot a graph of 1 on the y-axis against average temperature the plotting of the points may be more straightforward if you multiply all of the values for 1 t by a common factor (eg 104 ).
3.1.5.3 Effect of temperature on reaction rate
Required practical 3
Investigation of how the rate of a reaction changes with temperature.